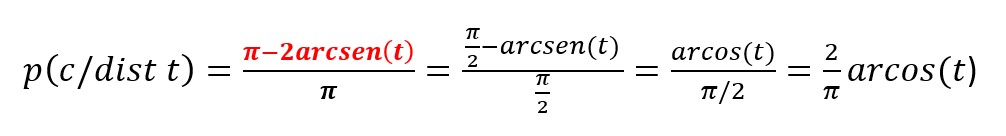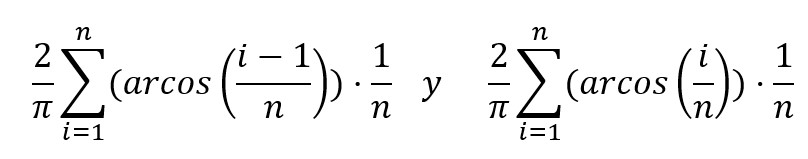CONCEPTO DE INTEGRAL. INTRODUCCIÓN CONSTRUCTIVA
Suma () v por las diferencias de t (dt)
Comenzamos con un ejemplo en el que realizaremos estas sumas, para concluir con lo que se escribe y se llama integral de v respecto de t.
Supongamos que hemos estado caminando 4 horas pero no sabemos qué distancia hemos recorrido, entonces empezamos a calcular según nuestro esfuerzo la velocidad que hemos podido llevar, en la primera hora fuimos a paso rápido, es decir, a 5 km/h. Pero en la segunda hora, ya más cansados, pensamos que la velocidad sería de 4 km/h. En la tercera hora íbamos charlando y la velocidad debió ser de 3 km/h Ya en la cuarta hora volvimos a andar a paso rápido, a 5 km/h. Estos datos se recogen en la siguiente tabla:
t en horas 1 2 3 4 v en km/h 5 4 3 5 ¿Cómo podemos saber la distancia recorrida?
Sumando las velocidades por el tiempo que duró cada una :
t en horas 1 2 3 4 v en km/h 5 4 3 5 en km 5 5+4=9 9+3=12 12+5=17 Para calcular el recorrido hemos realizado las suma de los valores de v por las diferencias de los valores de t.
Supongamos que hemos contado con un velocímetro que miramos cada media hora por lo que tenemos la siguiente tabla:
t en horas 0,5 1 1,5 2 2,5 3 3,5 4 v en km/h 5 5 3 5 2 4 4,5 5,5 Calculemos la distancia recorrida, hay que ir sumando las velocidades multiplicando por las diferencia de t:
t en horas 0,5 1 1,5 2 2,5 3 3,5 4 v en km/h 5 5 3 5 2 4 4,5 5,5 km 5·0,5 10·0,5 13·0,5 18·0,5 20·0,5 24·0,5 28,5·0,5 34·0,5 Si las mediciones de velocidad fueran cada minuto tendríamos el espacio recorrido en cada minuto y las suma de esos recorridos darán el recorrido total con más precisión. Cuando las diferencias de t se hacen tender a cero se tendrá el espacio recorrido con total precisión, es decir
Suma () v por las diferencias de t
cuando estas tienden a 0 (dt)
Observación 1: La derivada de la integral de v es igual a v
La derivada de una función S(t) se introduce como el límite cuando tiende a cero de . Si ahora hacemos las diferencias de la tercera fila de la tabla o valores de la integral entre las diferencias de t vemos que obtenemos v:
(13·0,5 - 10·0,5) / 0,5 = 3 (20·0,5 - 18·0,5) / 0,5 = 2
En ambos casos vemos obtemos v.
Por tanto la derivada de la integral de v es v. Por ello los matemáticos generalizando este concepto definen axiomáticamente la integral de v respecto de t como una primitiva de v, es decir, una función cuya derivada es v. De ahí que veamos la constante K al realizar integrales. En nuestro ejemplo se puede explicar como el punto kilométrico de donde parte el recorrido, que no tiene porqué ser 0.
Observación 2: La integral de la derivada de una función r es igual a r + K siendo K una constante
es igual a
cuyo total es r(la t donde acaban las sumas) - r(la t donde se inician las sumas).
Y como el límite cuando tiende a cero de la primera expresión es la integral, resulta:
Integral indefinida e integral definida
Podemos hablar de esta sumas sin definir el intervalo de t donde se realizan, es decir, sin determinar el principio y el fin, en ese caso se habla de integral indefinida. Cuando se define el principio y fin del intervalo se llamará integral definida.
Si en la observación 2 la integral está definida en [a b] vemos que el resultado es r(b)-r(a) lo cual se denota
Esta igualdad en la teoría reglada y axiomática de integrales se denomina teorema fundamental del cálculo integral.
Con el concepto de sumas ¿cuál es el valor de la integral de x y de la de x2
0 ... 0 ... La suma de los términos de la segunda fila es una progresión aritmética de diferencia , el primer término más el último es (0+x), y el número de términos es
Al multiplicar esta suma por resulta
Que cuando tiende a 0 esta expresión es igual a
En matemáticas se pueden hacer introducciones constructivas de los conceptos, si una vez realizada una introducción constructiva se ve la introducción axiomática, el concepto quedará enriquecido además de, en muchos casos, ganar belleza y comprensión del proceso de creación matemática.
Leibniz y Newton tuvieron que alcanzar el Summum al ver que este concepto les llevó a armonizar, la geometría, el cálculo de áreas, las derivadas... y todo se pudo axiomatizar (Cauchy). En el cálculo estadístico, en física, economía, geometría etc son imprescindibles las integrales. Estas Sumas se convirtieron en una teoría perfecta.
Hagamos otro cálculo de sumas, las de la función x2. A partir de este concepto de sumas hallaremos la integral de . Esta parte se puede y quizás se deba omitir en una introducción de la integral, pero tiene interés observar los conceptos con diferentes prismas y escoger en cada caso los cálculos más cómodos.
0 ... 0 ... La suma de los términos de la segunda fila por es igual a la suma de los cuadrados desde 1 a por
De la igualdad (n+1)3=n3+3n2+3n+1→ 3n2=(n+1)3-n3-3n-1 →
y al multiplicarlo todo por resulta
Así pues el triple de la suma de los términos de la segunda fila por cuando tiende a cero es
Es decir,
Este ejemplo deja patente la utilidad de las observaciones 1 y 2 que aseguran que estas sumas se calculan buscando una función cuya derivada sea la función que queremos o integrar.
Ejemplos de situaciones en las que aparecen estas sumas
Problema de estadística
La siguiente tabla recoge el resultado de un cuestionario de 4 preguntas. El 20% tuvo 4 aciertos, el 60% tuvo al menos 3 aciertos, etc.
F 20% 60% 85% 95% 100% v=nº de aciertos al menos 4 3 2 1 0 Calcula la
¿Qué representa este valor?
Solución
La suma es 4·20% + 3·40% + 2·25% + 1·10% + 0·5% = 0,8 + 1,2 + 0,5 + 0,1 = 2,6 que indica la media del número de aciertos en el grupo. Es decir, si el cuestionario fuera un examen que puntuara de 0 a 4, el grupo habría obtenido una nota media de 2,6, lo que sobre 10 en lugar de sobre 4 equivale a una nota media de 6,5. Good!
Problemas de límites
Calcular el límite cuando n tiende a infinito de
Solución
Sustituimos n porde modo que x es un número y tiende a cero. El límite pedido tiene esta expresión:
y al multiplicar el numerador y el denominador por obtemos que es igual a y en el límite cuando tiende a cero, es Cuyo valor es
Esto se puede hacer porque la primitiva que tomamos, , en cero vale cero. En el punto donde se empieza a contar, es decir en el punto de inicio de la primera fila en las tablas la primitiva tiene que valer 0.
Calcular el límite cuando n tiende a infinito de
Solución
Si multiplicamos los numeradores y denominadores por 1/n, que tiende a cero tenemos
Es decir,
que cuando tiende a cero es
Sirve esta primitiva pues en 0 que es el comienzo de x, vale 0: log|1 + 0| = 0.
Como sumamos solo hasta i=n, el último valor de x es n· 1/n que es 1, el resultado del límite es log| 1 + 1 | = log(2)
la tabla sobre la que se aplican las sumas y la integral es:
0 ... 1 ...
¿Conviene hacer introducciones constructivas en matemáticas?
Cuando me enseñaron las integrales, me las definieron como una función cuya derivada era la función a integrar, es decir, una primitiva. Pasé algún tiempo sin entender porqué esa notación, la S alargada era para mi un operador que significaba "primitiva de" luego se ponía la función y el dx significaba respecto de x, es decir la variable respecto la que derivábamos, pero no veía el significado de S como sumas y dx como diferencias de x. A veces el profesor me ponía un 0, con razón, porque se me olvidaba en el proceso multiplicar por dx, para mi sobraba, con la variable en la función ya poníamos respecto de qué variable integrábamos, es decir, en las derivadas se ponía f'(x), pues en la integral con Sf(x) no valía ¿por qué? A los pocos días con la integral definida ya se entendía la notación.
Ahora que los cálculos los hace inmediatamente un ordenador o un teléfono móvil quizás deberíamos dedicar algo de tiempo a calcular estas sumas, o a exponerlas y comprender el concepto, no es necesario ser ágiles en el cálculo de derivadas e integrales, el teléfono móvil integra con un clic. En general se dedica mucho tiempo a hacer "gimnasias matemáticas" más que a explicar ideas o conceptos.
Las gimnasias matemáticas ayudan muchas veces a entender los algoritmos o a aprenderlos. Aún así es sorprendente la falta de ejemplos de estas sumas en los textos, solo aparecen gráficamente con el cálculo de áreas y sin embargo estas sumas son frecuentes en los cálculos de muchas ramas científicas o como dicen los libros de texto "en la vida real", yo diría "en el mundo del cálculo frecuente".
¿Cuántos de los alumnos que terminan un bachillerato sabrían relacionar la media de una variable estadística con una integral? Creo que ni el 0,1% de los que saben calcular la integral de una función racional. "En el mundo del cálculo frecuente" ¿cuántos de nuestros alumnos se van a encontrar con una media y cuántos con la integral de (x+1)/(x2 - 4) "por dx"?
Cuando ya se conoce la teoría axiomática puede parecer una pérdida de tiempo mostrar la idea constructiva y considerar mejor opción mostrar el producto final que la construcción. En el arte queremos disfrutar de la escultura final. Pero la belleza de las matemáticas a veces no se concibe solo con el producto final que suele ser un método o un algoritmo, conocer la idea que promueve la teoría axiomática suele ser clave para poder contemplar con admiración y comprender ese resultado final. Las matemáticas son del mundo de las ideas, por tanto es importante conocer la idea motor de la teoría. El resultado final de un concepto matemático tiene que llevar consigo el proceso de creación, aunque muchas veces no sea el proceso real (que con frecuencia es farragoso). Se puede mostrar un proceso de creación esculpido, no solo el algoritmo o la teoría axiomática.
La mayor parte de los alumnos que terminan un bachillerato no conocen la teoría axiomática ni la constructiva del cálculo integral, eso sí, aprenden a calcular integrales de funciones que no aparecerán nunca ni en ingeniería, ni en informática, economía o medicina, solo en exámenes de matemáticas. Esto en una época en la que se puede calcular cualquiera de esas integrales con apretar un botón de nuestro teléfono móvil. Es más probable que estos futuros profesionales al investigar en su campo tengan que integrar una función de la que solo conocen los datos recogidos, es decir una función de la que solo se conocen los datos de una tabla, son más probables estas situaciones que la integración de una función de la que conoce la expresión algebraica.
Consolación Ruiz Gil Enero 2017
Aguja de Buffon
Este problema con su solución está descrito en la wikipedia lo desarrollaremos pensando que se pueda comprender en un segundo de bachillerato. Nos centramos en el caso de agujas de longitud 2 y unas líneas paralelas cuya distancia es también de 2 unidades.
EL PROBLEMA
Se lanza un palillo de 2 u de longitud sobre un suelo entarimado cuyas tablas miden 2 u de ancho. Demostrar que la probabilidad de que el palillo cruce alguna de las juntas es 2/п
EXPLICACIÓN
1 Calculemos la probabilidad de que el palillo cruce alguna de las juntas (suceso c) sabiendo que su centro está a una distancia t de la junta que tiene más cerca (suceso dist t). Hallaremos p(c/dist t)
Estando el centro del palillo a una distancia t de la junta, los casos favorables para cada lugar del centro son los que el extremo cae en la parte señalada en rojo y los casos posibles son toda la semicircunferencia,
2 Calculemos la probabilidad de que el centro del palillo esté a menos de una distancia t de la junta más cercana
los casos favorables son aquellos señalados en rojo, su área es 2t· ancho· número de juntas = 2t· ancho· largo/2 (pues 2 es la distancia entre dos juntas). Por tanto los casos favorables ocupan un área igual a t· ancho· largo
y los casos posibles ocupan un área igual a ancho· largo
Así pues la probabilidad es igual a t
3 Probabilidad de que la mínima distancia del centro del palillo a una junta sea entre (i-1)/n y (i/n) siendo n un número natural y i también número natural pero menor o igual que n
Esta probabilidad es igual a 1/n
4 Probabilidad que el palillo cruce una junta sabiendo que la mínima distancia de su centro a una junta está entre (i-1)/n y (i/n)
Como la distancia del centro a la junta más cercana será mayor que (i-1)/n y menor que i/n pues según el punto 1 esta probabilidad, p(c/ dist entre (i-1)/n y (i/n)) está acotada por los valores de p(c/dist (i-1)/n) y p(c/dist i/n):
5 La probabilidad de que cruce una junta y la mínima distancia del centro a una junta esté entre entre (i-1)/n y (i/n)
Esta probabilidad es el producto de la condicionada, calculada en el punto 4 y la probabilicad calculada en el punto 3, luego está comprendida entre
,
Por último la probabilidad de que el palillo cruce alguna junta es igual a las suma de estas probabilidades cuando i varía de 1 a n, pues el centro estará en alguna de las franjas, así pues estará comprendida entre
Por fin ya concluimos que la probabilidd de que el palillo cruce una junta es
Consolación Ruiz Gil Enero 2024